先日ご紹介した、
コンパスのみで円周を4分割して下さい(中心が与えられた円)
の解答編です。
面白く、よく出来た問題です。
通称「ナポレオンの問題」と呼ばれているそうです。
中心が与えられていない円の4分割場合はもっと難しく「真のナポレオンの問題」と呼ばれているらしいです。
本文は、中心が与えられた円を4分割する場合の問題です。
ちょっとだけヒント。というかコンパスの定義。
コンパスでは直線が引けないことに注意。←これ当たり前ですが。
・中心が取れる円が描ける。
・線分の長さを移せる。
—
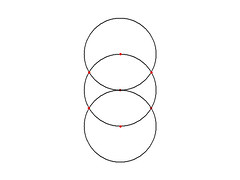
↑ここまでだと6分割。ここから補助円とかを引きまくると…。
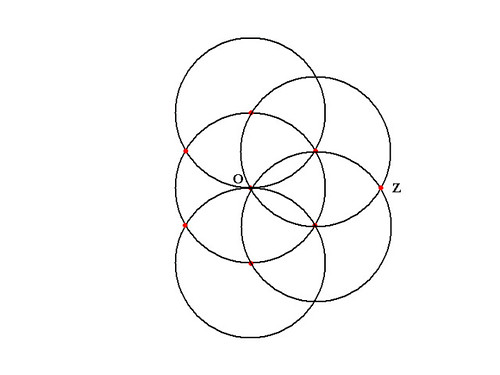
↑ここまでやってOとZに線を引けば終了!その直線と点Oを中心とする円の交点が引ければそれを4回やれば4分割だよ!……ところが直線が引けないんです!コンパスのみだから!
というところで堂々巡りを繰り返す…。
下記の図の直線は分かりやすく説明するための補助線です。
↓
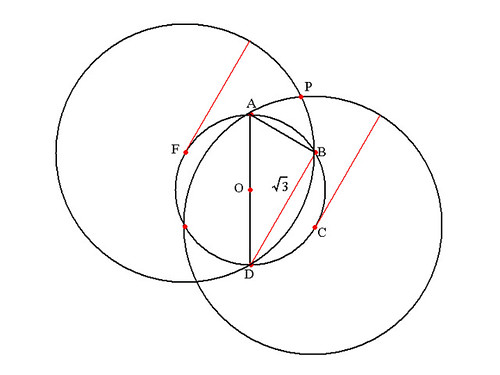
直径の両点と円周を通る点の3点は円周を通る点を直角とした直角3角形。
AO=AB、AD=2AO
(補足:点Bは上記の円の6分割の際にプロットした点。半径AOでプロットしたのでAO=AB)
よって三平方の定理によりBD=√3
2^2=1^2+x^2
4=1+x^2
x=√3
(点Oを中心とし半径AOで円Oを書き、その長さを維持したまま今度はAを中心とし円を書き、円Oとの交点をB、点Bを中心とし…と繰り返すと点C、点Fもプロットできる)
上記のようにして出来た√3をコンパスで拾って点C、点Fを中心とした円を書く。2つの円の交点をPとする。
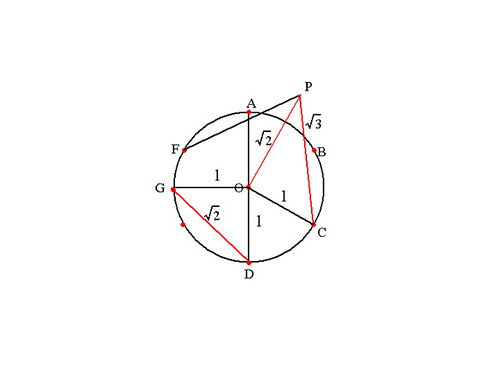
CFは直線。点C点Fより同じ長さの点Pとその中点Oなので、POとCFは直交。
よって3角形OCPは直角3角形。
OC=1、PC=√3なので三平方の定理でOP=√2
(√3)^2=1^2+y^2
3=1+y^2
y=√2
√2をコンパスで拾って点Dを中心として円を書く。円Oとの交点をGとすると三平方の定理で角DOGは直角。
これをあと3回やれば4分割となる。
結構長い。
でもコンパスでのみ、なのに3平方の定理を使いまくり、なのが面白い。
↑
spoiler
よって4分割。
結構長い…。


コメント